определить промежутки возрастания и убывания функции.Найти экстремумы функции y=e^x^3-3
определить промежутки возрастания и убывания функции.Найти экстремумы функции y=e^x^3-3
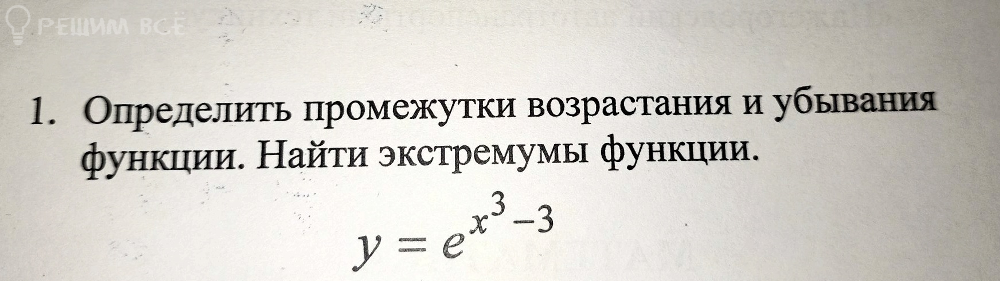
Похожие вопросы
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки в течение 1 года
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Поможем написать учебную работу




































Для нахождения промежутков возрастания и убывания функции, а также экстремумов, необходимо найти производную функции и найти ее нули.
Итак, дана функция y = e^(x^3) - 3. Найдем производную этой функции:
y' = (e^(x^3))' = 3x^2 * e^(x^3)
Теперь найдем нули производной:
3x^2 * e^(x^3) = 0
Так как экспонента никогда не равна нулю, то нулями производной будут точки, где 3x^2 = 0, то есть x = 0. Это единственная точка, в которой производная равна нулю.
Теперь рассмотрим знак производной на интервалах (-∞, 0) и (0, +∞). Возьмем произвольные значения для x в этих интервалах (например, x = -1 и x = 1):
При x = -1: y' = 3(-1)^2 e^((-1)^3) = 3e^(-1) > 0
При x = 1: y' = 31^2 e^(1^3) = 3e > 0
Таким образом, производная положительна на интервалах (-∞, 0) и (0, +∞). Это значит, что функция возрастает на всей области определения.
Теперь найдем экстремумы функции. Так как функция возрастает на всей области определения, это означает, что у функции нет ни точек максимума, ни точек минимума.
Итак, промежутки возрастания функции: (-∞, +∞)
Промежутки убывания: отсутствуют
Экстремумов нет.