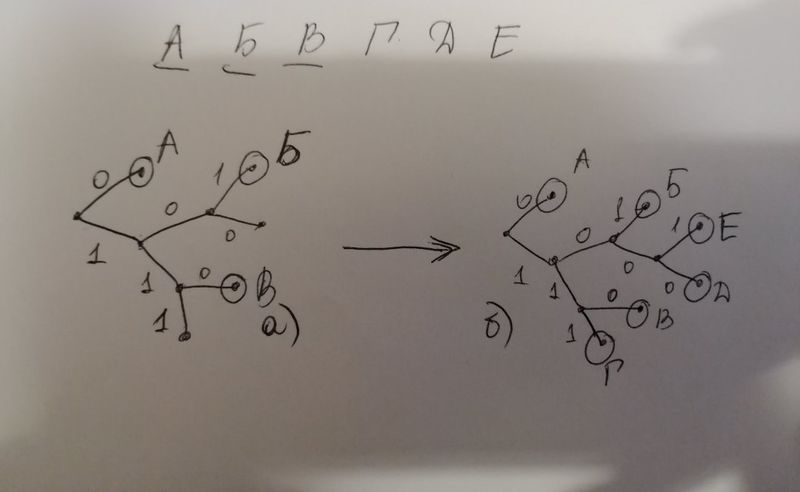
Можно составить дерево, где обознаить уже имеющиеся символы. Если символ взят, то продолжать дерево в том месте мы не можем. (Чтобы выполнялось условие Фано.) см. рисунок. Каждой вершине дерева соответствует свое число, и все эти числа вместе будут удовлетворять условию Фано. В вершине можно либо остановиться, и взять соответствующее число как кодировку некоторого символа, либо продолжить дерево, сделав две новые ветки: 0 или 1. Как мы видим, взять длину 3 для оставшихся 3-х букв не получится (см. а)), придется раздвоить одну из 2-х оставшихся вершин(см. б)) Получается, что для двух из 3-х незакодированных символов нам потребуется кодировка длиной 4 (на рисунке это символы "Е" и "Д"), и еще одну можем взять длиной 3 (на рисунке это символ "Г").

Теперь, когда мы нашли оптимальный сппособ кодировки, посчитаем суммарную длину: длина кодового слова для А = 1, Б = 3, В = 3, Г = 3, Д = 4, Е = 4. Итого: 1 + 3 + 3 + 3 + 4 + 4 = 18.

Примечание: не важно, какой символ с каким кодовым словом мы сопоставляем, потому что нам важна только длина этих кодовых слов.