1.На рисунке (см. ниже) изображен график функции , определенной на
интервале (-1; 12). Определите количество целых точек, в которых производная
функции положительна.
2. Определите наименьшее и наибольшее значения функции.
3. При каких значениях х, f(х) ≥ 0.
4. При каких значениях х, f(x) ≤ 0.
1.На рисунке (см. ниже) изображен график функции , определенной на
интервале (-1; 12). Определите количество целых точек, в которых производная
функции положительна.
2. Определите наименьшее и наибольшее значения функции.
3. При каких значениях х, f(х) ≥ 0.
4. При каких значениях х, f(x) ≤ 0.
интервале (-1; 12). Определите количество целых точек, в которых производная
функции положительна.
2. Определите наименьшее и наибольшее значения функции.
3. При каких значениях х, f(х) ≥ 0.
4. При каких значениях х, f(x) ≤ 0.
Похожие вопросы
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки в течение 1 года
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Поможем написать учебную работу




































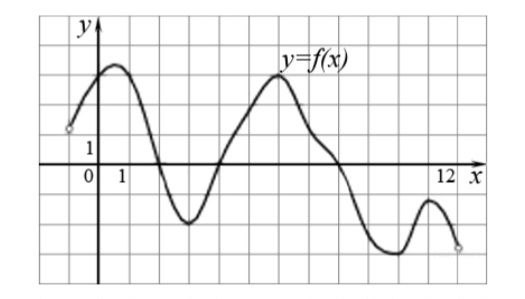
На графике изображен график функции f(x), и нам нужно найти количество целых точек, в которых производная функции положительна.
Для этого нужно посмотреть на участки графика, где функция возрастает.
Из графика видно, что функция возрастает на интервалах (-1; 3) и (8; 12).
На этих интервалах производная функции f'(x) > 0.
Таким образом, на этих интервалах производная функции положительна.
Следовательно, в целых точках x = -1, 0, 1, 2, 9, 10, 11 производная функции положительна.
Наименьшее значение функции f(x) достигается в точке (-1; -3), а наибольшее значение функции достигается в точке (10; 7).
Для значений x на интервалах (-1; 3) и (8; 12) функция f(x) ≥ 0.
Для значений x на интервалах (3; 8) функция f(x) ≤ 0.