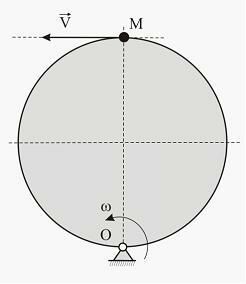
Диск радиуса R=4 м вращается с постоянной угловой скоростью 2 рад/с вокруг оси, проходящей через точку О перпендикулярно плоскости чертежа. По ободу диска движется точка М с постоянной относительной скоростью V=4м/с. Найти абсолютную скорость точки (м/с) в момент наибольшего удаления точки М от оси вращения.
Диск радиуса R=4 м вращается с постоянной угловой скоростью 2 рад/с вокруг оси, проходящей через точку О перпендикулярно плоскости чертежа. По ободу диска движется точка М с постоянной относительной скоростью V=4м/с. Найти абсолютную скорость точки (м/с) в момент наибольшего удаления точки М от оси вращения.
Похожие вопросы
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки в течение 1 года
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Поможем написать учебную работу




































Для начала запишем данные задачи:
Радиус диска ( R = 4 ) мУгловая скорость диска ( \omega = 2 ) рад/сОтносительная скорость точки ( M ) по ободу диска ( V = 4 ) м/сРассмотрим, как будет выглядеть абсолютная скорость точки ( M ) в момент наибольшего удаления от оси вращения. Наибольшее удаление точки ( M ) от оси вращения происходит, когда она находится на краю диска, т.е. на расстоянии ( R ) от оси.
Нам нужно найти компоненты абсолютной скорости точки ( M ):
Компонента скорости за счёт вращения:
[
V_{\text{rotation}} = R \cdot \omega = 4 \, \text{м} \cdot 2 \, \text{рад/с} = 8 \, \text{м/с}
]
Эта скорость направлена перпендикулярно радиусу, в этом случае она будет направлена по касательной к окружности.
Компонента скорости за счёт перемещения точки ( M ):
Это относительная скорость точки ( M ) по ободу диска, которая задана параметром ( V = 4 ) м/с.
Теперь нам нужно сложить эти две скорости. Поскольку скорость вращения и скорость движения по ободу направлены в одну сторону (по касательной), мы можем просто сложить их:
[
V{\text{absolute}} = V{\text{rotation}} + V = 8 \, \text{м/с} + 4 \, \text{м/с} = 12 \, \text{м/с}
]
Таким образом, абсолютная скорость точки ( M ) в момент наибольшего удаления от оси вращения равна:
[
\boxed{12 \, \text{м/с}}
]
Для начала запишем данные задачи:
Радиус диска ( R = 4 ) мУгловая скорость диска ( \omega = 2 ) рад/сОтносительная скорость точки ( M ) по ободу диска ( V = 4 ) м/с
Рассмотрим, как будет выглядеть абсолютная скорость точки ( M ) в момент наибольшего удаления от оси вращения. Наибольшее удаление точки ( M ) от оси вращения происходит, когда она находится на краю диска, т.е. на расстоянии ( R ) от оси.
Нам нужно найти компоненты абсолютной скорости точки ( M ):
Компонента скорости за счёт вращения:
[
V_{\text{rotation}} = R \cdot \omega = 4 \, \text{м} \cdot 2 \, \text{рад/с} = 8 \, \text{м/с}
]
Эта скорость направлена перпендикулярно радиусу, в этом случае она будет направлена по касательной к окружности.
Компонента скорости за счёт перемещения точки ( M ):
Это относительная скорость точки ( M ) по ободу диска, которая задана параметром ( V = 4 ) м/с.
Теперь нам нужно сложить эти две скорости. Поскольку скорость вращения и скорость движения по ободу направлены в одну сторону (по касательной), мы можем просто сложить их:
[
V{\text{absolute}} = V{\text{rotation}} + V = 8 \, \text{м/с} + 4 \, \text{м/с} = 12 \, \text{м/с}
]
Таким образом, абсолютная скорость точки ( M ) в момент наибольшего удаления от оси вращения равна:
[
\boxed{12 \, \text{м/с}}
]