Найти частные производные первого и второго порядков функции трех переменных
Найти частные производные первого и второго порядков функции трех переменных
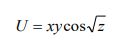
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки в течение 1 года
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Поможем написать учебную работу




































Для нахождения частных производных функции трех переменных сначала найдем частные производные по каждой переменной по отдельности.
Пусть дана функция f(x, y, z).
Частная производная по переменной x:
∂f/∂x = (∂f/∂x, ∂f/∂y, ∂f/∂z)
Частная производная по переменной y:
∂f/∂y = (∂f/∂x, ∂f/∂y, ∂f/∂z)
Частная производная по переменной z:
∂f/∂z = (∂f/∂x, ∂f/∂y, ∂f/∂z)
Для нахождения частных производных второго порядка нужно взять частные производные первого порядка и снова продифференцировать их по каждой переменной.
Например, частная производная второго порядка по переменным x и y:
∂²f/∂x∂y = (∂/∂x(∂f/∂y), ∂/∂y(∂f/∂x), ∂/∂z(∂f/∂x))
Аналогично можно найти частные производные второго порядка по другим переменным.
Таким образом, для нахождения частных производных первого и второго порядков функции трех переменных, необходимо последовательно вычислять частные производные по каждой переменной и их комбинации.