Стороны равнобедренного треугольника равны 13, основание равно 24. Найти радиус вписанной и описанной окружности
Стороны равнобедренного треугольника равны 13, основание равно 24. Найти радиус вписанной и описанной окружности
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки в течение 1 года
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Поможем написать учебную работу




































В равнобедренном треугольнике стороны равны a = 13, основание b = 24.
Найдём радиус вписанной окружности.
r = 24/2 * √(2 * 13 - 24)/(2 * 13 + 24) = 12 * √(2 : 50) = 12 * 1/5 = 2,4.
Найдём радиус описанной окружности по формуле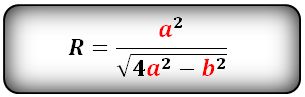
R = 13 * 13/√(4 * 13 * 13 - 24 * 24) = 13 * 13/√(676 - 576) = 169/10 = 16,9
Ответ: r = 2,4; R = 16,9.