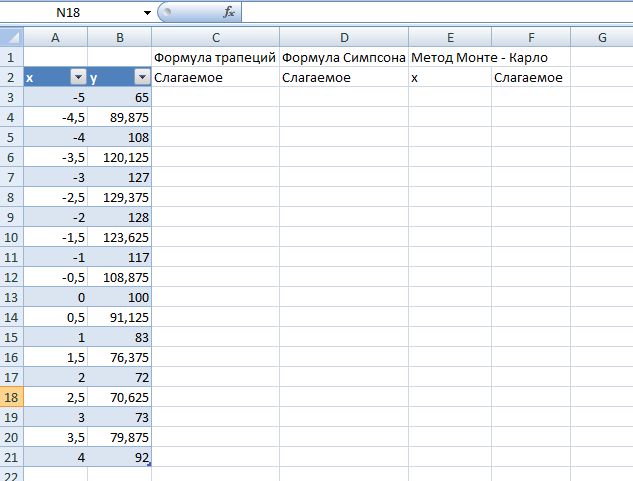
Для начала построим график функции y = x^3 - 18x + 100 на интервале [-5, 4]:

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-5, 4, 100)
y = x*3 - 18x + 100

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('График функции y = x^3 - 18x + 100')
plt.grid(True)
plt.show()

Далее найдем значения a и b, где функция пересекает ось x (y=0):

a = -3
b = 2

Теперь вычислим площадь криволинейной трапеции тремя способами.

По формуле трапеций:
h = (b - a)/2
S_trapez = h * (f(a) + f(b))
def f(x):
return x*3 - 18x + 100

S_trapez = h * (f(a) + f(b))
print(f'Площадь трапеции по формуле трапеций: {S_trapez}')

По формуле Симпсона:
S_simpson = h/3 (f(a) + 4f((a+b)/2) + f(b))
print(f'Площадь трапеции по формуле Симпсона: {S_simpson}')

Методом Монте-Карло:
n = 100000
x_rand = np.random.uniform(a, b, n)
y_rand = np.random.uniform(0, f(a), n)
count = 0
for i in range(n):
if y_rand[i] <= f(x_rand[i]):
count += 1

S_monte_carlo = (b - a) f(a) count / n
print(f'Площадь трапеции методом Монте-Карло: {S_monte_carlo}')