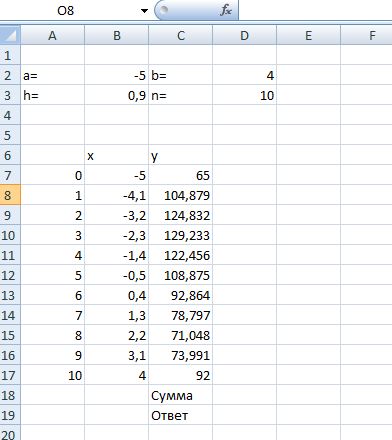
Помогите составить формулы для Exel, по которым можно вычислить площадь криволинейной трапеции, ограниченной линиями y= x^3-18x+100, диапазон изменения аргумента [-5;4], тремя способами: по формуле трапеций; по формуле Симпсона; методом Монте-Карло.
Помогите составить формулы для Exel, по которым можно вычислить площадь криволинейной трапеции, ограниченной линиями y= x^3-18x+100, диапазон изменения аргумента [-5;4], тремя способами: по формуле трапеций; по формуле Симпсона; методом Монте-Карло.
Похожие вопросы
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки в течение 1 года
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Поможем написать учебную работу




































Формула для вычисления площади криволинейной трапеции по формуле трапеций:
=S*(f(a)+f(b))/2
где S - разница между значениями функции в точках a и b, f(a) и f(b) - значения функции в точках a и b соответственно.
Для данной функции и диапазона изменения аргумента [-5;4], формула будет выглядеть следующим образом:
=S((A3^3-18A3+100)+(A4^3-18*A4+100))/2
где A3=-5, A4=4.
Формула для вычисления площади криволинейной трапеции по формуле Симпсона:
=(S/3)(f(a)+4f((a+b)/2)+f(b))
где S - разница между значениями функции в точках a и b, f(a) и f(b) - значения функции в точках a и b соответственно, f((a+b)/2) - значение функции в точке (a+b)/2.
Для данной функции и диапазона изменения аргумента [-5;4], формула будет выглядеть следующим образом:
=(S/3)((A3^3-18A3+100)+4((A3+A4)/2)^3-18((A3+A4)/2)+100+(A4^3-18*A4+100))
где A3=-5, A4=4.
Для метода Монте-Карло требуется использовать случайную выборку точек в заданном диапазоне и вычислить значение функции в этих точках. По формуле площади криволинейной трапеции можно вычислить площадь, усреднив значения функции в выбранных точках.
Например, можно использовать следующую формулу в Excel для метода Монте-Карло:
=AVERAGE(FUNCTION(A5:A100))
где A5:A100 - случайная выборка точек в диапазоне [-5;4], FUNCTION - формула функции y= x^3-18x+100.
Эти формулы помогут вам вычислить площадь криволинейной трапеции ограниченной линией y= x^3-18x+100 тремя различными способами.